Unlocking the Hidden Gems of Data Structures: A Walkthrough of 6 Overlooked Essentials
This article examines six underrated data structures—such as Tries, Fenwick Trees, and Splay Trees—exploring their mechanics, advantages, drawbacks, and real-world applications to help developers expand their problem-solving toolkit.
Most developers stick to familiar data structures like arrays, hash maps, and binary trees. But for specific problems, other lesser-known structures can provide unique advantages. In this article, we’ll dive into six underrated data structures, explore how they work, evaluate their strengths and weaknesses, and examine their real-world applications.
1. Trie (Prefix Tree)
Summary:
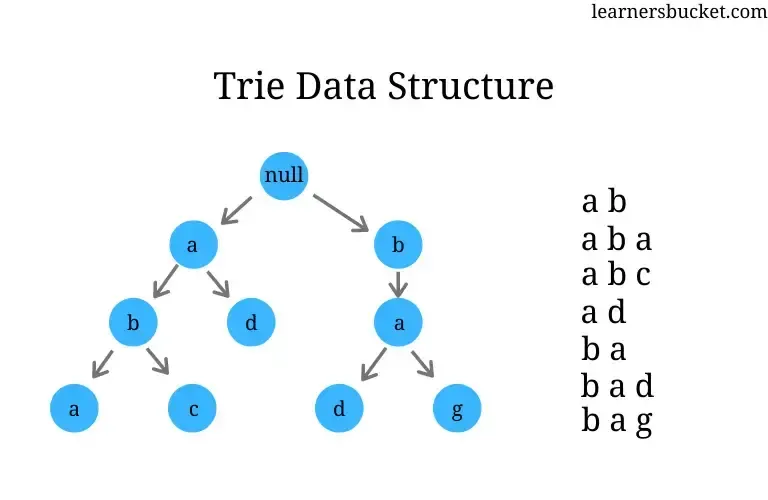
A Trie (pronounced “try”) is a tree-like data structure used to store strings. It’s particularly suited for scenarios requiring efficient prefix-based operations, such as autocomplete systems. Each node represents a single character, and paths from the root to leaf nodes form strings.
How It Works:
-
Structure:
A Trie starts with a root node, and each edge represents a character. Nodes may store additional metadata, such as whether a string ends at that node. -
Insertion:
To insert a word like “cat”:- Start at the root.
- For each character in “cat,” create a child node if it doesn’t already exist.
- Mark the last node as the end of a word.
-
Search:
To search for “cat”:- Traverse the Trie character by character.
- If you successfully reach the last character node, “cat” exists in the Trie.
-
Prefix Search:
To find all words starting with “ca”:- Navigate to the node for “ca.”
- Perform a depth-first search to gather all words in the subtree.
Pros:
- Efficient Lookups: Supports fast searches, insertions, and prefix-based queries in O(L), where L is the string length.
- Autocomplete Ready: Ideal for predictive text applications.
Cons:
- High Memory Usage: Requires significant space when storing many strings with few common prefixes.
- Implementation Complexity: Needs careful design to balance memory and speed.
Real-Life Usage:
- Search Engines: Power autocomplete and suggestion features.
- Dictionary Management: Store and search dictionaries for spelling corrections.
- IP Routing: Match hierarchical addresses in networking.
2. Fenwick Tree (Binary Indexed Tree)
Summary:
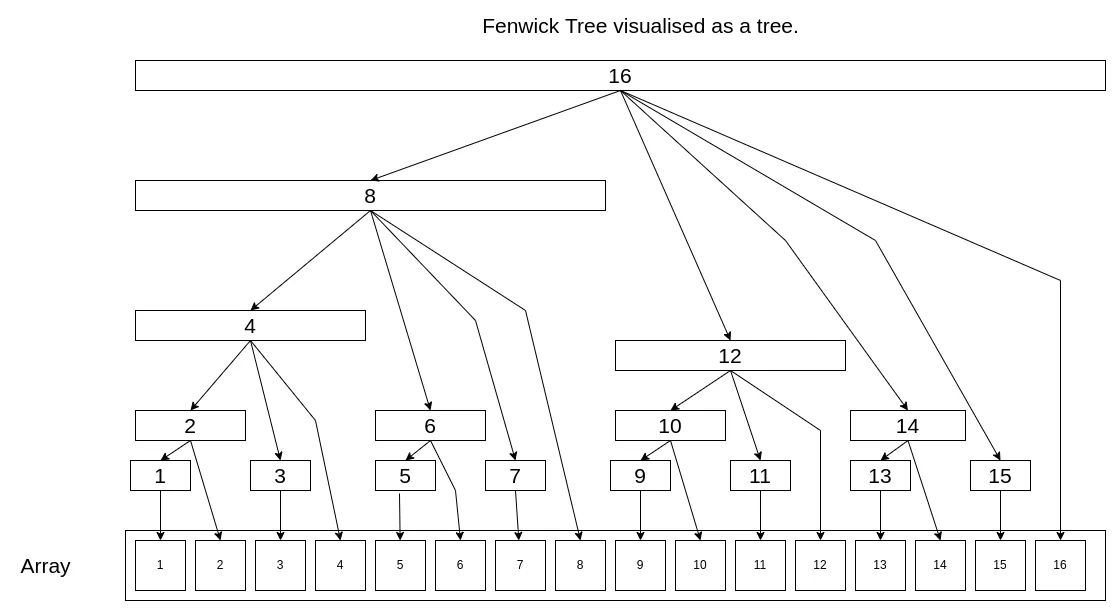
A Fenwick Tree is a compact data structure used for efficient prefix sum queries and updates in an array. It avoids recomputation of sums from scratch, making it faster than naive methods.
How It Works:
-
Structure:
A Fenwick Tree is implemented as a 1D array where each index stores cumulative sums for specific ranges of elements. These ranges are determined by the binary representation of indices, with each index representing sums over increasingly larger ranges. -
Indexing:
The binary representation of indices determines how updates and queries traverse the tree.- Query (Prefix Sum): Move to parent indices by iteratively subtracting the least significant bit (LSB).
- Update: Propagate changes to overlapping ranges by adding the LSB to the current index.
Operations:
- Construction: Build the tree from an array in O(N log N).
- Query: Compute prefix sums in O(log N) by traversing the tree.
- Update: Reflect changes in O(log N) by updating relevant indices.
Pros:
- Efficient: Queries and updates in O(log N).
- Space-Saving: Uses O(N) memory.
Cons:
- Specialized: Limited to numeric range queries.
- Non-General: Unsuitable for non-linear operations like min or max.
Real-Life Usage:
- Gaming Leaderboards: For dynamic rankings.
- Range Queries: In financial or statistical applications.
- Competitive Programming: A favorite for prefix-sum problems.
3. Disjoint Set (Union-Find)
Summary:
The Disjoint Set, also known as Union-Find, manages collections of non-overlapping sets. It’s often used for dynamic connectivity problems, such as determining whether two elements belong to the same group.
How It Works:
-
Initialization:
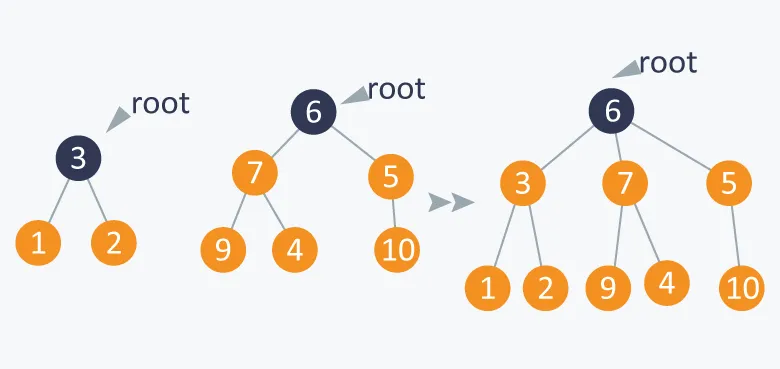
Each element starts in its own set. The parent array stores the “leader” of each set, and a rank array keeps track of tree depth for efficiency. -
Find Operation:
Find the representative of an element’s set using path compression, which flattens the tree structure for faster lookups. -
Union Operation:
Merge two sets by connecting their leaders. Use rank (or size) to ensure the smaller set is attached to the larger one, keeping the tree shallow.
Pros:
- Fast Operations: Nearly constant time for both union and find with path compression.
- Simple and Lightweight: Minimal memory usage.
Cons:
- Narrow Focus: Designed for problems involving connected components or equivalence relations.
- No Iteration: Cannot directly iterate over set members.
Real-Life Usage:
- Graph Algorithms: Used in Kruskal’s MST algorithm.
- Network Connections: Manage connected components in a network.
- Clustering: Identify groups of related items.
4. Bloom Filter
Summary:
A Bloom Filter is a probabilistic structure for checking membership in a set. It’s fast and space-efficient, but allows false positives (indicating an element is present when it’s not).
How It Works:
-
Bit Array:
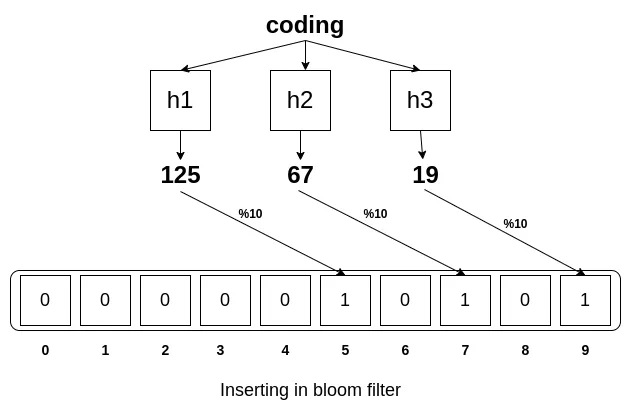
Initialize a bit array of size m to zeros. -
Hash Functions:
Use k independent hash functions to map an element to k indices in the bit array. -
Insert Operation:
Hash the item and set the corresponding indices in the bit array to 1. -
Lookup Operation:
Hash the queried item and check if all corresponding bits are 1. If any bit is 0, the item is definitely absent.
Pros:
- Space-Efficient: Requires less memory compared to storing the set explicitly.
- Fast: Insertion and lookup are O(K), where K is the number of hash functions.
Cons:
- False Positives: May incorrectly report the presence of an element.
- No Deletion: Once a bit is set, it cannot be unset without introducing errors.
Real-Life Usage:
- Web Caching: Quickly check if data is cached.
- Databases: Test for key existence before fetching from disk.
- Spam Detection: Efficiently filter known spam emails.
5. Skip List
Summary:
A Skip List is an augmented linked list with multiple levels of pointers, allowing faster searches, insertions, and deletions.
How It Works:
-
Levels:
Each node can belong to one or more levels. Higher levels “skip” over multiple nodes for faster traversal. -
Insertion:
Insert the element into the base level. Randomly decide how many additional levels the node should participate in. -
Search:
Start at the top level and move downwards, narrowing the search range.
Pros:
- Balanced Performance: O(log N) on average for search, insertion, and deletion.
- Simplicity: Easier to implement compared to balanced trees.
Cons:
- Extra Memory: Requires additional pointers for higher levels.
- Randomization Dependency: Performance relies on good randomness.
Real-Life Usage:
- Databases: Used in Redis for maintaining sorted sets.
- Indexing: Manage dynamic sorted lists efficiently.
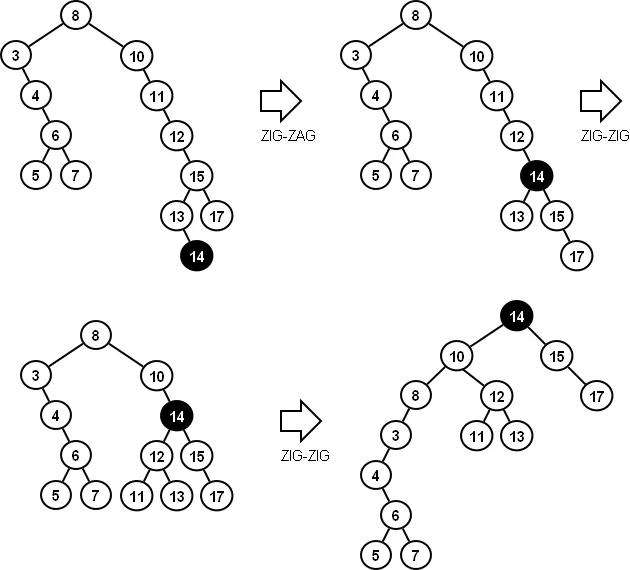
6. Splay Tree
Summary:
A Splay Tree is a self-adjusting binary search tree. It brings frequently accessed elements closer to the root, optimizing for non-uniform access patterns.
How It Works:
-
Splay Operation:
After any access (search, insert, or delete), the accessed node is moved to the root using tree rotations. -
Search/Insert/Delete:
Operate like a regular BST, but with a splay step afterward.
Pros:
- Self-Optimizing: Adapts to usage patterns, making frequently accessed elements quicker to retrieve.
- Simple Balance: Maintains approximate balance without explicit balancing.
Cons:
- Variable Performance: Worst-case time is O(N) for a single operation.
- Rotations Overhead: Frequent rotations can be computationally expensive.
Real-Life Usage:
- Caches: Adaptive data structures for frequently accessed items.
- String Manipulation: Speed up substring operations in text editors.
For more details, visit Splay Tree: One Tree to Rule Them All.
Conclusion
| Data Structure | Key Strength | Drawback | Best Application |
|---|---|---|---|
| Trie | Fast prefix-based search | Memory-intensive | Autocomplete, spell-checking |
| Fenwick Tree | Efficient prefix sums | Specialized for sums | Gaming leaderboards, range queries |
| Disjoint Set | Dynamic connectivity | Limited to connected components | Network clustering |
| Bloom Filter | Space-efficient membership tests | False positives | Web caching, spam detection |
| Skip List | Balanced performance for sorted data | Randomization dependency | Databases, priority queues |
| Splay Tree | Self-adjusting, frequent access | Rotational overhead | Adaptive caches, text editors |
These data structures are hidden gems that, when used correctly, can solve specific problems more efficiently than standard options. Explore them to level up your problem-solving toolkit!
All the implementations can be found here.